Algoritmos basicos en machine learning. 2. Regresión logística

Regresión logística: - La regresión logística es un algoritmo de clasificación basado en la función que se utiliza en el  método: la función logística o función sigmoidea. 

Es una curva en forma de S que se utiliza para predecir un resultado binario (1/0, Sí / No, Verdadero / Falso) dado un conjunto de variables independientes.

También se puede considerar como un caso especial de regresión lineal cuando la variable de salida (Y) es categórica, donde usamos el logaritmo de probabilidades como variable dependiente (X).

Predice la probabilidad de ocurrencia de un evento ajustando los datos a una función logit.

p (X) = e ^ (b0 + b1 * X) / (1 + e ^ (b0 + b1 * X)) 

bo (intercepto) y b1 son los coeficientes del modelo

X variable independiente

Y variable dependiente

Ejemplo: Se tiene un experimento con ratones en donde la variable dependiente de salida es categórica: Obeso o No Obeso. La regresión logística se parecería a lo que se muestra en la figura de abajo:

Python, graficar datos categoricos

Cuando exploramos datos pensamos en variables con números pero que sucede con la exploración de variables que no son numéricas (por ejemplo, sexo, usa o no usa internet, le gusta o no le gusta un alimento, etc). Son las llamadas variables categóricas.

Las dos categorías principales de datos categóricos son nominales y ordinales.

En el atributo de datos categóricos nominales, no existe el concepto de ordenar entre los valores de ese atributo.

Los atributos categóricos ordinales tienen algún sentido o noción de orden entre sus valores.

Los gráficos que se utilizan generalmente para visualizar este tipo de datos son

• grafico de barras
• grafico de conteo
• diagrama de caja
• enjambre
• diagrama de factores

Antes de continuar, importemos algunos datos de muestra con los que jugaremos. Usemos un conjunto de datos de muestra "Sugerencias" que brinde información sobre las facturas de un restaurante.

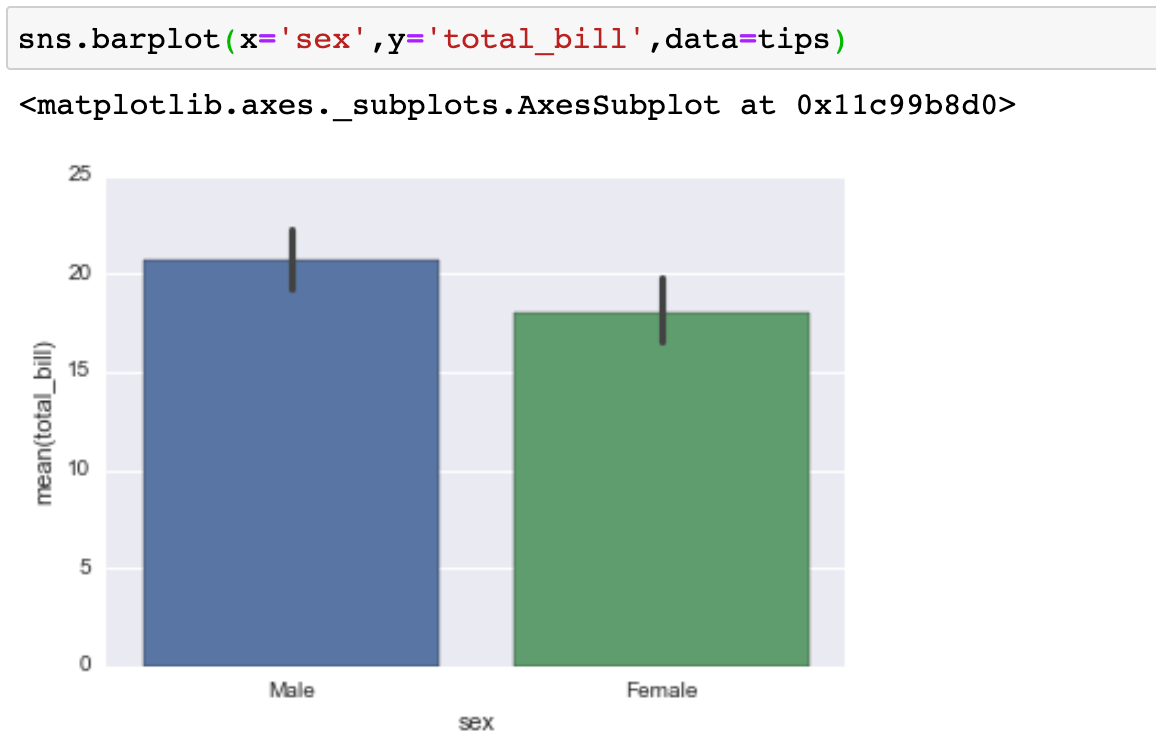
Grafico de Barras

Esta gráfica le permite obtener datos agregados de una característica categórica en sus datos. El ** barplot ** es un gráfico general que le permite agregar los datos categóricos basados en alguna función, por defecto la media:

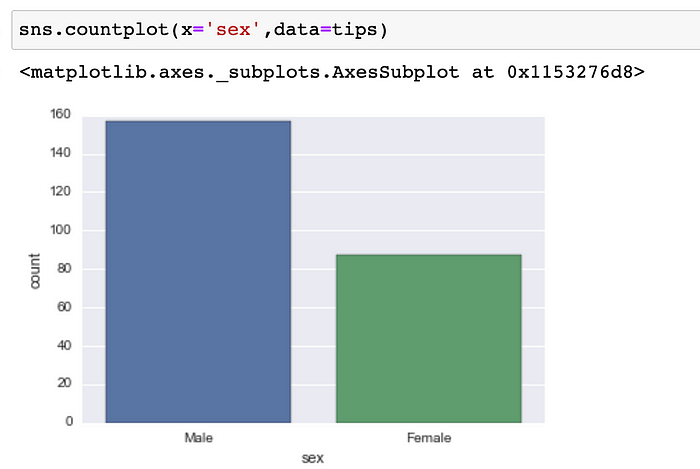
Grafico de conteo (Countplot):

Esto es esencialmente lo mismo que el diagrama de barras, excepto que el estimador está contando explícitamente el número de ocurrencias. Es por eso que solo pasamos el valor x:

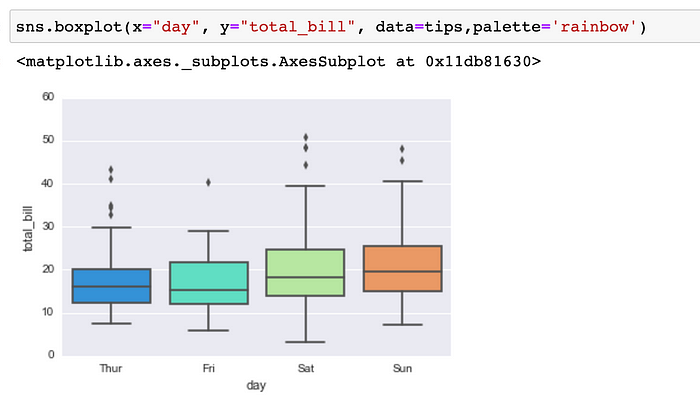
Diagrama de caja:

Un diagrama de caja es una forma estandarizada de mostrar la distribución de datos basada en un resumen de cinco números (“mínimo”, primer cuartil (Q1), mediana, tercer cuartil (Q3) y “máximo”).

Grafico de enjambres (Swarmplot):

Swarmplot: los puntos se ajustan (solo a lo largo del eje categórico) para que no se superpongan. Esto proporciona una mejor representación de la distribución de valores, aunque no escala tan bien a un gran número de observaciones (tanto en términos de la capacidad de mostrar todos los puntos como en términos del cálculo necesario para organizarlos).

Diagrama de factor:

factorplot es la forma más general de un diagrama categórico. Puede tomar un parámetro ** tipo ** para ajustar el tipo de gráfico: (variando el Kind en el cèdigo se puede cambiar de un tipo de grafico a otro)

COmo puede ver el grafico obtenido con factorplot es exactamente igual al obtenido con barplot, ya que kind = bar en el còdigo.

basado en: https://medium.com/@gauravdahiya/visualising-categorical-data-8fe887c98e57

REGRESION LINEAL EXPLICADA

En un post anterior comenté sobre el algoritmo básico y mejor entendido del machine learning: la regresión lineal. 

El análisis de regresión es una metodología estadística que permite determinar la fuerza de la relación de dos variables. La regresión no se limita a dos variables, se pueden utilizar más de dos variables. 

Los resultados de la regresión ayudan a predecir un valor desconocido en función de la relación con las variables de predicción. Por ejemplo, la altura y el peso de una persona suelen tener una relación. Generalmente, las personas más altas tienden a pesar más. Podríamos usar el análisis de regresión para ayudar a predecir el peso de un individuo, conociendo su altura.

Cuando hay una sola variable de entrada, la regresión se denomina Regresión lineal simple. Se utiliza la variable única (independiente) para modelar una relación lineal con la variable objetivo (dependiente). Esto se hace ajustando un modelo para describir la relación. 

Si hay más que una variable de predicción, la regresión se denomina Regresión lineal múltiple.

Cuando se intenta encontrar la "línea de mejor ajuste", el modelo de regresión se le llama Regresión de mínimos cuadrados ordinarios. Esto significa que se está utilizando la suma más pequeña de errores al cuadrado. El error es la diferencia entre el valor de y predicho restado del valor de y real. La diferencia se eleva al cuadrado, por lo que hay una diferencia absoluta y se suma.

Coeficientes de regresión

Al realizar una regresión lineal simple, los cuatro componentes principales son:

• Variable dependiente, X, : la variable objetivo / será estimada y predicha
• Variable independiente ,Y: variable predictora / utilizada para estimar y predecir
• Pendiente: ángulo de la línea / indicado como "m" ò  𝛽1
• Intercepto: donde la función cruza el eje y / se indica como c o 𝛽0
• La ecuación de regresión puede expresarse como (ambas formas son vàlidas):
• Y = m + cX     
• Y = 𝛽0 + 𝛽1 X

Los dos últimos, pendiente e intercepto, son los coeficientes / parámetros del modelo de regresión lineal, De lo que se trata es de encontrar la línea recta (entre un número infinito de líneas) que mejor se ajuste a los datos. 

R-cuadrado / coeficiente de determinación (R-squared)

El objetivo de la regresión lineal es encontrar la "línea de mejor ajuste" que describe los datos. Sin embargo,  la línea encontrada no representa completamente la relación entre las variables ya que habrà error entre el valor medido y el predicho (y_medido - y_predicho). El coeficiente R-Cuadrado se usa para determinar qué tan bien se ajusta un modelo a los datos. Este coeficiente también se conoce como coeficiente de determinación. 

Python, leer un archivo

Para leer el contenido de un archivo, primero debes abrirlo usando la función global open (), que acepta 2 parámetros: la ruta del archivo y el modo.

Para leer, use el modo de lectura (r):

filename = '/Users/rafaondata/prueba.txt'

file = open(filename, 'r')

#or

file = open(filename, mode='r')

Una vez que tenga el archivo abierto, puede usar los métodos read () para leer todo el contenido del archivo en una cadena:

content = file.read()

También puede optar por leer el contenido una línea a la vez:

line = file.readline()

Es común combinar esto con un bucle, por ejemplo, para leer cada línea en una entrada de lista:

filename = '/Users/rafaondata/prueba.txt'

file = open(filename, 'r')

while True:
    line = file.readline()
    if line == '': break
    print(line)

Al final del procesamiento de su archivo, recuerde cerrar el archivo:

file.close()

Algoritmos basicos en machine learning. 1 REGRESION LINEAL

Este es el primero de una serie de posts sobre algoritmos de machine learning (ML) que se utilizan comúnmente en data science o ciencia de datos

La regresión lineal es el algoritmo más conocido y mejor entendido en estadística y aprendizaje automático. La regresión lineal es un modelo lineal, es decir, un modelo que asume una relación lineal entre las variables de entrada (x) y la variable de salida única (y), lo que significa que y se puede calcular fácilmente usando la relación lineal.

Cuando hay una sola variable de entrada (x), la ecuación se denomina regresión lineal simple.

Cuando hay más de una variable de entrada, la ecuación se denomina regresión lineal múltiple.

La ecuación y = a + b1 * x (donde x es la variable de entrada, y es la variable de salida y a y b son los coeficientes) representa gráficamente una regresión lineal(ver figura) 

La recta de la regresión se encuentra minimizando las distancias al cuadrado entre los puntos y la línea de mejor ajuste y esto se conoce como minimizar la suma de los residuos al cuadrado. Los residuos se definen simplemente como el valor predicho (por la ecuación de regresión) menos el valor real.

En el próximo post (lunes próximo) explicaré con más detalle la regresión lineal

Python, cómo escribir en un archivo

Para escribir contenido en un archivo, primero debe abrirlo usando la función global open (), que acepta 2 parámetros: la ruta del archivo y el modo.

Puede usar a como el modo, para decirle a Python que abra el archivo en modo append (anexar) y agregue contenido al archivo

filename = '/Users/rafaondata/test.txt'

file = open(filename, 'a')

#or

file = open(filename, mode='a')

O puede usar el "flag" w para borrar el contenido existente:

filename = '/Users/rafaondata/test.txt'

file = open(filename, 'w')

#or

file = open(filename, mode='w')

Una vez que tenga el archivo abierto, puede usar los métodos write () y writelines ().

write () acepta una cadena.

writelines () acepta una lista de cadenas:

filename = '/Users/rafaondatatest.txt'

file = open(filename, 'w')

file.write('This is a line\n')

file.writelines(['One\n', 'Two'])

file.close()

Recuerde cerrar un archivo después de escribir en él, usando el método close () del archivo.

Python, guía de estilo PEP8

Cuando se escribe código, deben usarse las convenciones del lenguaje de programación que se utiliza.

Si aprende las convenciones correctas de nomenclatura y formato desde el principio, otras personas encontrarán su código más fácil de leer.

Python define sus convenciones en la guía de estilo PEP8. PEP son las siglas de Python Enhancement Proposals y es el lugar donde ocurren todas las mejoras y discusiones del lenguaje Python. Hay muchas propuestas de PEP, todas disponibles en https://www.python.org/dev/peps/.

La Guía PEP8 define el formato y algunas reglas sobre cómo escribir Python de forma “pitónica”.

Puede leer su contenido completo aquí: https://www.python.org/dev/peps/pep-0008/ pero aquí hay un resumen rápido de los puntos importantes con los que puede comenzar:

• Aplicar sangría mediante espacios, no tabulaciones
• Sangra usando 4 espacios.
• Los archivos de Python están codificados en UTF-8
• Utilice un máximo de 80 columnas para su código
• Escriba cada declaración en su propia línea
• Las funciones, los nombres de las variables y los nombres de los archivos están en minúsculas, con guiones bajos entre las palabras (snake_case)
• Los nombres de las clases están en mayúscula, las palabras separadas también se escriben con la letra mayúscula, (CamelCase)
• Los nombres de los paquetes están en minúsculas y no tienen guiones bajos entre las palabras.
• Las variables que no deben cambiar (constantes) se escriben en mayúsculas
• Los nombres de las variables deben ser significativos
• Agregue comentarios útiles, pero evite los comentarios obvios
• Agregar espacios alrededor de los operadores
• No use espacios en blanco innecesarios
• Agregar una línea en blanco antes de una función
• Agregar una línea en blanco entre los métodos de una clase
• Dentro de las funciones / métodos, las líneas en blanco se pueden usar para separar bloques de código relacionados para ayudar a la legibilidad